| |
Eximius Diu slide rule, v1
|
Home Slide Rules Accuracy Linear Circular Cylindrical Eximius Diu Guestbook
Eximius Diu 6 - version 1, May 2012 (now superseded)
I've built an improved Eximius Diu 6, but have retained the web page of the old one here for comparison.
|
Eximius Diu 6 - version 1, May 2012
Spiral slide rules are more compact than
linear and cylindrical ones for very long scales. They have the
added advantage that the inner turns of the slide rule are shorter
than the outer turns. If we arrange the scale so that the numbers
increase from inner to outer, and the inner spiral turn is one tenth
the diameter of the outer, then the accuracy will be the same at the
beginning and end of the spiral. The accuracy is about the same
(slightly better) within the interior of the spiral.
I wrote a computer program to generate an
image of the spiral, add markers and text at the correct logarithmic
locations along the spiral, and add some colors etc. Ignoring the
irony that it took a computer to generate the slide rule (though
it's quite possible to generate the slide rule manually as it
would have been done in the old days), the result is a usable slide
rule that is accurate to 6 decimal places across its whole range.
You need to be very careful to get that last digit of accuracy.
The slide rule was printed at 600 dpi on A0 paper, then trimmed and
laminated. The spiral diameter is 750 mm (29.5"),
with 135 spiral turns giving a scale length of 175 m (574
ft). Due to the nature of spiral slide rule scales, this is
equivalent to a linear slide rule of length 318 m
(1043 ft). In other words, a linear or straight slide rule would
need to be 318 m long in order to have the same 6 digits minimum accuracy
at all points: Linear slide rules are 10 times more accurate
at the low end near 1 than at the top end near 10, whereas a
spiral slide rule can compromise by making the accuracy more
constant from end to end.
For a more detailed explanation of slide rule accuracy see... Slide rule accuracy
Two additional sheets of clear plastic film were cut
to the diameter of the spiral, scored with a pin to make a very thin
marker line from the centre to the edge, and pinned over the laminated
printout to become the equivalent of the two cursors. |
Using the Eximius Diu slide rule
There are three layers to the slide rule:
the printed and laminated image, and two overlaid transparent
layers. Each transparent layer has a very fine line etched from the
centre to the outside of the spiral. A pin is pushed
through the three layers so that the etched line
in each transparent layer can be rotated independently. If this had ever
been made as a commercial unit it would have to be made
more robust, but the pin does a fine job fine of demonstrating
the principle.
 |
The Eximius Diu 6 slide rule laid out on a
table. The spiral is 750mm diameter (about 30"), printed on paper
and laminated. Above that are two transparent circular
layers called Cursor A and Cursor B. All three are pinned
through their centers so that the two cursor layers can be
independently rotated. Each of the two cursor layers has a
thin line from the centre to the outside. See the clothes peg
at the bottom, used to hold either the two cursor layers,
or all three layers, in position.
Click the image for a larger
view.
|
 |
The three layers centred with the pin,
so that the two etched lines can be rotated. Call the first
transparent layer "Cursor A" and the top one "Cursor B". I used another two layers of
blank laminate - they weren't quite as transparent as I'd
hoped, so some of the images are a little cloudy.
Click the image for a larger view. You
will see the pin sticking up, and the two very thin and somewhat faint cursor lines - Cursor A
heading up towards 1 (pointing at about 1 o'clock in
the image), and Cursor B at about 5 o'clock.
|
 |
Doing a calculation - let's try 1.23456 * 4.56789. The correct
answer to 6 decimal places is 5.63933. First align Cursor A
so that its etched line goes through 10 (it will also go
through 1 and the centre).
|
 |
Keeping Cursor A fixed over 10, rotate Cursor B to pass
through the first multiplicand (1.23456).
|
 |
Fix Cursors A and B together (e.g. using pegs or
clips) so that we can rotate them together around the slide
rule without changing their position relative to each other.
We need to preserve the angle between the two etched
lines.
Rotate Cursors A and B together until Cursor A's line goes
through the second multiplicand (4.56789)
|
 |
Now Cursor B's line will pass through the solution, we just
need to find which turn of the spiral is the correct
one.
|
 |
The simplest way to find the spiral loop that the answer
lies on is to take a regular slide rule and calculate the
approximate answer. You could do it by counting rings, but
it's easier with the regular slide rule. The pic shows a Faber
Castell 52/82 calculating 1.234* 4.57 to be about 5.64, so
we know the answer is around there.
|
 |
Back to the Eximius Diu 6, we can
easily see which is the correct loop of the spiral to use, and
we can (very carefully) estimate the result to be about 5.63932. Click the image to enlarge it to see the
red arrow. The correct answer is 5.63933, so we were pretty close here,
and within the 6 decimal places
accuracy.
|
|
Some low res images
The slide rule is a bit big to show here at its full resolution (at 600 dpi and 18,000 x 18,000 pixels the png file size is 28MB).
Meanwhile here are a few lower resolution images, starting with
the whole slide rule, diameter 750 mm. Click on the image to see it at about actual size, but with the resolution reduced to 120 dpi.
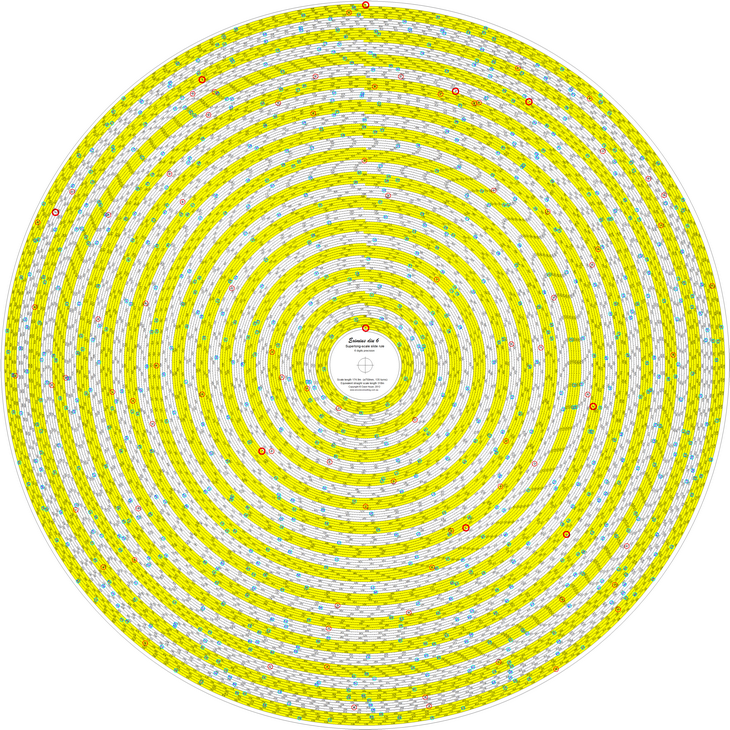
|
About actual size, resolution reduced to 120 dpi. Use the scroll bars to scroll the image...
|
Zoomed in the area around 10..
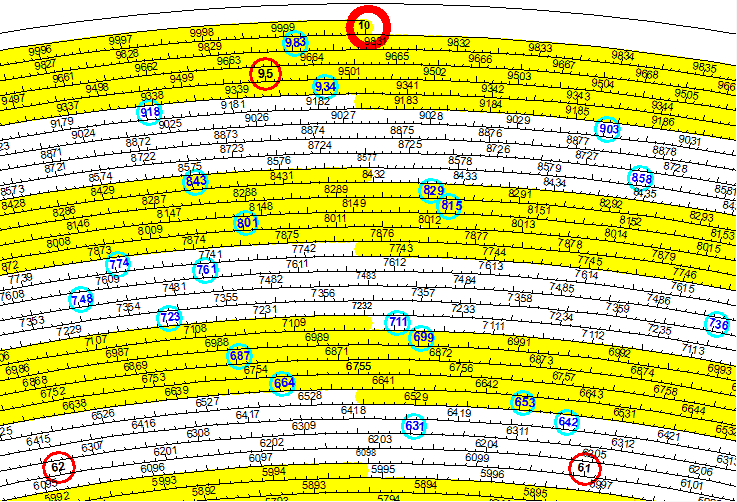
|
Zoomed in the area around 1..
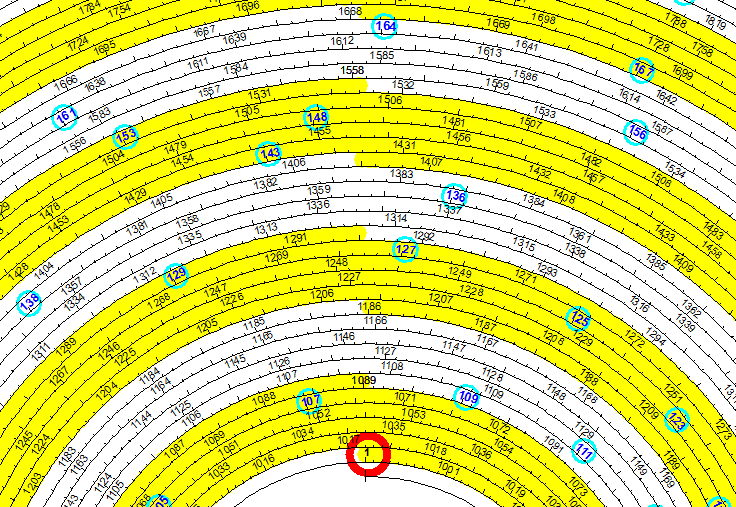
|
Make your own Eximius Diu 6 v1.. (note that this is an older version)
Download a high resolution (600 dpi) PDF file
that you can print and laminate. Print it on A0 or similar size
paper, sized so that the diameter of the spiral is 750 mm (about
30"). Then laminate it. Then make two additional transparent layers,
cut them to a circular shape just large enough to cover the
whole slide rule spiral. Mark both transparent layers with a very
fine line from the centre to the periphery (I used a pin to scratch
along a steel rule, then a non-permanent marker along the scratch,
then wipe the excess leaving a very fine black line in the scratch).
Pin the three layers carefully through the exact center, and you're
ready to go. As an alternative to a pin, you might also consider
using a CD/DVD case similar to that show by Ying Hum here. Let me know if you find a better way
of doing the cursor.
Download EximiusDiu6-v1-D750mm-T135-L175m-600dpi.pdf
(22 MB). Please note this pdf is copyright. It can be downloaded and
printed freely for
any use. Please
give acknowledgement if distributing it. If
you make one of these, I'd be interested to know - just drop a note in
the guest book. Dave Hoyer, Dec 2012.
Update, Aug 2013. I've made up a new version that will be more practical to use. This includes a different color layout
to help guide the eye to the numbers being sought, a circular slide rule around the outer edge for the initial estimate, and
more practical acrylic cursors. See EximiusDiu6 v2 |
| Copyright © 2013, Dave Hoyer. |
|